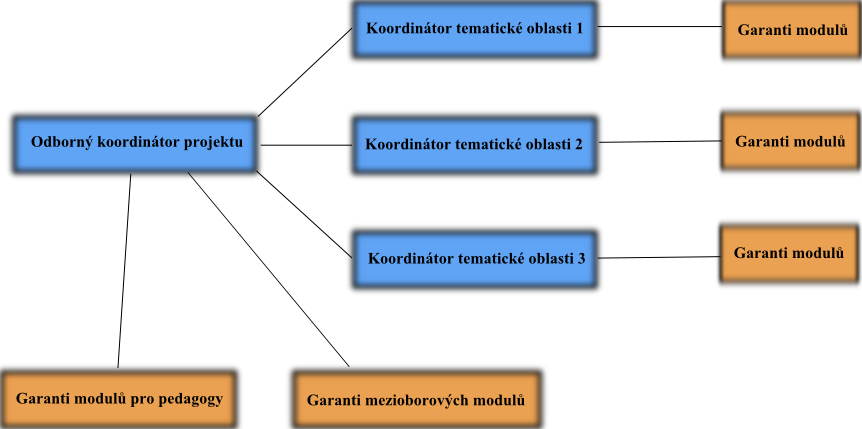
Organizační struktura
Koordinátoři tematických oblastí a jejich moduly
Koordinátoři tematických oblastí koordinují vytváření základních a specializovaných matematických modulů, které jsou členěny dle zaměření do následujících tematických oblastí.
- Tematická oblast 1: Matematická analýza – Jiří Bouchala
- Tematická oblast 2: Lineární algebra, numerické metody a metody optimalizace - Oldřich Vlach
- Tematická oblast 3: Diskrétní matematika, teorie grafů a statistika – Petr Kovář
Za všechny moduly z dané tematické oblasti zodpovídá Koordinátor tematické oblasti. Ten bude v průběhu tvorby výukových modulů kontrolovat jejich obsah, grafickou stránku a jejich vzájemnou provázanost (používání stejné terminologie, odkazy na využití daného pojmu v jiném modulu, zařazení praktických ukázek z odborných předmětů atd.).
Koordinátor tematické oblasti | Název modulu | Garant |
J. Bouchala | Diferenciální počet funkcí více proměnných | P. Šarmanová |
Integrální počet funkcí více proměnných | P. Vodstrčil | |
Interaktivní sbírka úloh k integrálnímu počtu funkcí více proměnných | P. Šarmanová | |
Parciální diferenciální rovnice | G. Holubová | |
Úvod do funkcionální analýzy | J. Bouchala | |
Variační metody | J. Bouchala | |
Funkce komplexní proměnné | J. Bouchala | |
Diskrétní transformace | D. Horák | |
| Integrální transformace | T. Kozubek | |
Obyčejné diferenciální rovnice | B. Krajc | |
Matematické modelování elektromagnetických polí | D. Lukáš | |
Herbář funkcí | P. Nečesal | |
Prostory funkcí a řešitelnost základních typů PDR | P. Girg | |
Řady | J. Bouchala | |
Křivkový a plošný integrál | J. Bouchala | |
O. Vlach | Lineární algebra s Matlabem | T. Kozubek |
Numerické metody 1 | V. Vondrák | |
Matematické modelování a metoda konečných prvků (Numerické metody 2) | R. Blaheta | |
Metody optimalizace | Z. Dostál | |
Analytická geometrie | L. Šindel | |
Numerické modelování v hydrologii | M. Brandner | |
Lineární algebra | Z. Dostál | |
P. Kovář | Vybrané kapitoly z pravděpodobnosti | M. Litschmannová |
| Úvod do statistiky | M. Litschmannová | |
Základy diskrétní matematiky | M. Kubesa | |
Úvod do teorie grafů | P. Kovář | |
Teorie grafů | P. Kovář | |
Základy teorie čísel a jejich aplikací pro nematematiky | P. Jahoda |
Odborný koordinátor projektu a jeho moduly
Odborný koordinátor řídí vytváření všech mezioborových modulů:
| Název modulu | Garant |
Z. Dostál | Teoretická elektrotechnika II | P. Orság |
Řešení obvodů grafy signálových toků | J. Punčochář | |
Pružnost a pevnost | R. Halama | |
Metoda konečných prvků a metoda hraničních prvků | M. Fusek | |
Matematika v pozadí řešení inženýrských úloh | J. Szweda | |
Pružnost a plasticita | M. Krejsa | |
Spolehlivost a bezpečnost staveb | M. Krejsa | |
Základy matematické teorie pružnosti | A. Materna | |
Metoda konečných prvků | A. Materna | |
Matematické základy počítačové grafiky | E. Sojka | |
Matematické základy digitálního zpracování obrazů | E. Sojka | |
Matematické základy kryptografických algoritmů | E. Ochodková |
Odborný koordinátor koordinuje také vytváření všech modulů pro pedagogy.